Разрежение разведочной сети является одним из методов обоснования ее рациональной геометрии (размеров ячейки и ее пространственной ориентировки). Необходимость его применения отмечается в требованиях ГКЗ (1). Указанный метод, в сравнении с другими подходами, обладает следующими существенными преимуществами:
- результаты не зависят от принятой математической (статистической) модели;
- результаты отражают природные особенности (изменчивость) свойств объекта;
- характеризует действительную связь между критерием разведанности и параметрами (геометрией) сети.
Несмотря на длительную историю и имеющийся опыт применения данного метода (2) его эффективность оказывается крайне низкой при решении практических задач разведки. Выбор параметров разведочной сети на его основе производится в исключительно редких случаях. Во многом это положение объясняется отсутствием единых (стандартных) подходов к интерпретации результатов разрежения.
Трудности в разработке таких подходов определяются:
- отсутствием установленных количественных критериев разведанности;
- отсутствием установленных предельных величин критериев и методики их вычисления для запасов разных категорий;
- неопределенностью объемов недр, на которые следует распространять полученные оценки.
Под критериями разведанности следует понимать количественные показатели, величина которого определяется природными особенностями объекта и параметрами (геометрией) разведочной сети. В течение длительного времени в среде отечественных и ряда зарубежных геологов-разведчиков обсуждаются два критерия:
- точность (погрешность) оценки запасов или средних значений геологоразведочных параметров;
- ошибки в определении пространственного положения оруденения (ошибки геометризации);
Точность вывода геологоразведочных параметров, особенно средних содержаний полезных компонентов, определяет экономические риски, связанные как с общей геолого-экономической оценкой объекта, так и с планированием и проведением эксплуатационных работ в определенные периоды времени.
Ошибки геометризации определяют экономические риски, связанные с принятием технических решений по обоснованию контуров отработки (открытых и подземных работ) и по выбору систем отработки. Кроме того, они влияют на оценку потерь и разубоживания в процессе эксплуатации.
Предельные значения этих критериев для разных категорий запасов неоднократно предлагались различными исследователями, что отражено в разведочной литературе, в том числе в документах ГКЗ (4). В Рекомендациях ГКЗ (2008г) имеется положение, важное для практического применения данных критериев: объектом оценки является блок, сопоставимый с годовой производительностью предприятия.
Наибольшее внимание исследователей привлекают, требования к точности (ошибкам) оценки средних значений параметров, особенно средних содержаний полезных компонентов. Вместе с тем, для предлагаемых предельных значений погрешностей зачастую не указываются способы их вычисления. В одних случаях можно предполагать, что авторами рассматриваются средние значения относительных отклонений, а в других случаях – среднеквадратичные относительные отклонения. В ряде работ прямо указывается, что ошибки оцениваются через коэффициент вариации при разных уровнях доверительной вероятности. Величина критерия Стьюдента ta при этом изменяется, как правило, от 1 до 2. Указанные разногласия создают существенные трудности для использования данного критерия геологами-практиками.
Для унификации подходов предлагается все оценки точности параметров вычислять на основе стандартных (среднеквадратичных) отклонений при условии использования единого уровня доверительной вероятности а= 0,68 (значение критерия Стьюдента ta = 1). Средние относительные погрешности, вычисляемые при разрежении сети, могут быть приведены к значениям относительных среднеквадратичных ошибок с использованием поправочного коэффициента 1.2. При необходимости эти показатели легко пересчитываются применительно к любой доверительной вероятности.
Основные положения методики проведения исследований и интерпретации результатов разрежения применительно к оценке точности сводятся к следующему:
- оценка средних параметров и запасов в пределах участка детализации, на котором проводится разрежение;
- определение соотношения К между запасами в блоке годовой производительности Vгп и запасами в участке детализации Vуч; (К = Vгп /Vуч);
- определение и учет собственной ошибки исходной модели;
- учет всех вариантов наложения разреженной сети; вычисление средних погрешностей;
- пересчет на относительные среднеквадратичные ошибки с учетом поправочного коэффициента 1.2 и собственной ошибки модели;
- пересчет среднеквадратичных ошибок для сетей разной геометрии (плотности) Pуч на ошибки, применимые к блоку годовой производительности Pгп: Pгп = Pуч/ ;
- сравнение полученных значений с предельными величинами, установленными для запасов разных категорий;
Исходными материалами для проведения исследований и определения ошибок геометризации методом разрежения сети могут являться результаты сопровождающей эксплуатационной разведки или данные по участкам детализации, разведанным с шагом не более 5-10м. Использование сети с меньшей исходной плотностью потребует введения поправок за собственную погрешность модели, методика расчета которых пока детально не разработана.
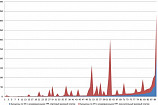
Предельные величины ошибок геометризации для рудных месторождений установлены эмпирически на основе изучения достаточно большого количества объектов (3). Для запасов категории С1 в разрезах (сечениях) она не должна превышать 50%. Для плоских сечений (проекций) она не превышает 30%. Результаты определения ошибок геометризации при разрежении сети обычно отображаются на графиках.
Обоснование плотности разведочной сети с позиций ошибок геометризации имеет особое значение для угольных месторождений, месторождений строительных материалов, агрохимического сырья, коренных месторождений алмазов.
При формулировке итоговых выводов о рациональности той или иной сети необходимо иметь ввиду, что предельные значения критериев могут различаться для разных видов минерального сырья; их определение является задачей дальнейших исследований в данном направлении.
Особенности применения данной методики могут быть рассмотрены на примере золоторудного месторождения, представленного пологозалегающими рудными телами. Исследования проводились на участке детализации, где была создана сеть скважин колонкового бурения 15х15м при их общем количестве 318 шт. (рис.1). Кондиционное оруденение вскрыто в 174 скважинах. Для получения единых значений параметров в каждой точке наблюдения после выделения интервалов выполнялся расчет суммарных характеристик – мощности, содержания и метрограмма по каждому разведочному пересечению.

Рис. 1. Участок детализации, сеть колонкового бурения 15*15 м.
Для обоснования рациональной плотности разведочной сети были проведены исследования по ее разрежению с параметрами:15х30м, 30х30м и 30х60м; рассмотрено соответственно 2, 4 и 8 вариантов наложения. В процессе разрежения исследовались два показателя разведанности месторождений – точность (погрешность) оценки геологоразведочных параметров и ошибки геометризации.
Величина собственных ошибок в оценке параметров зависит от плотности исходной разведочной сети и числа разведочных пересечений по ней, а также характера изменчивости свойств объекта. Максимальные значения этих ошибок могут определяться через оценку дисперсии признака и дисперсию среднего значения признака. Результаты расчета таких (максимальных) значений приведены в таблице 1.
| параметр | содержание | мощность | метрограмм |
| дисперсия | 1,351 | 72,992 | 448,690 |
| стандартное отклонение | 1,162 | 8,54 | 21,18 |
| коэффициент вариации | 0,533 | 0,635 | 0,722 |
| относит. стандарт среднего | 0,04 | 0,0483 | 0,0549 |
| относительная дисперсия | 0,0016 | 0,00233 | 0,003 |
Таблица 1. Расчет собственной ошибки модели
Относительное стандартное отклонение, определяющее собственную ошибку модели, рассчитано как частное от деления коэффициента вариации на корень квадратный из числа наблюдений (174). Оно составляет для разных параметров от 4,0 до 5.5%. В нижней строке таблицы рассчитана относительная дисперсия среднего значения признака, которая участвует в дальнейших расчета при введении поправок в величину ошибок.
По исходной сети оценены подсчетные параметры и запасы руды и золота на участке детализации; определены значения средней мощности руды по пересечениям и величина средней продуктивности (метрограмма). Величина объемной массы сухой руды на месторождении составляет 1.83 т/м3. Аналогичным образом эти же показатели определены по каждому из вариантов наложения разреженной сети. Результаты разрежения приведены в таблице 2.
|
Результаты разрежения сети |
||||||||||
| сеть | нач.точка | вариант | число | сод. | сумма.м | сумма мс | ср.м | ср.мс | руда, тт | золото, кг |
| исход. | 174 | 2,185 | 2238,1 | 4890,5 | 12,9 | 28,1 | 921,5 | 2013,7 | ||
| 15х30 | 62-24 | 1 | 87 | 2,196 | 1079,4 | 2370,6 | 12,4 | 27,2 | 888,9 | 1952,2 |
| 62-25 | 2 | 87 | 2,175 | 1158,7 | 2519,9 | 13,3 | 29 | 954,2 | 2075,1 | |
| 30х30 | 63-27 | 1 | 45 | 2,132 | 642,4 | 1369,5 | 14,3 | 30,4 | 1058 | 2255,6 |
| 63-28 | 2 | 42 | 2,228 | 516,3 | 1150,4 | 12,3 | 27,4 | 850,3 | 1894,7 | |
| 62-24 | 3 | 47 | 2,165 | 546,3 | 1183,1 | 11,6 | 25,2 | 899,8 | 1994,7 | |
| 62-25 | 4 | 40 | 2,228 | 533,1 | 1187,6 | 13,3 | 29,7 | 878 | 1955,9 | |
| 30х60 | 62-25 | 1 | 26 | 2,069 | 298,7 | 618 | 11,5 | 23,8 | 983,9 | 2035,7 |
| 62-24 | 2 | 21 | 2,242 | 276,9 | 620,7 | 13,2 | 29,6 | 912,1 | 2044,6 | |
| 63-27 | 3 | 20 | 2,116 | 276 | 584,1 | 13,8 | 29,2 | 909,1 | 1924,1 | |
| 63-28 | 4 | 18 | 2,092 | 223,3 | 496 | 12,4 | 26 | 735,6 | 1634 | |
| 64-30 | 5 | 21 | 2,282 | 247,6 | 565,1 | 11,8 | 26,9 | 815,6 | 1861,4 | |
| 64-31 | 6 | 19 | 2,213 | 256,2 | 566,9 | 13,5 | 29,8 | 843,9 | 1867,3 | |
| 65-30 | 7 | 25 | 2,143 | 366,4 | 785,4 | 14,7 | 31,4 | 1206,9 | 2587 | |
| 65-31 | 8 | 24 | 2,332 | 293 | 683,4 | 12,2 | 28,5 | 965,1 | 2251 | |
Табл. 2. Результаты разрежения сети.
Из данных таблицы видно, что средние содержания характеризуются достаточно высокой устойчивостью при разных вариантах разрежения. На основе данных таблицы 2 по основным параметрам подсчета – среднему содержанию, запасам руды и запасам золота определены погрешности их оценки по вариантам наложения сети. Результаты этих расчетов приведены в таблице 3. Для сети каждой плотности определены величины средних отклонений параметров и относительных средних отклонений. Для приведения их значений к величинам стандартных отклонений, которые применяются при всех статистических расчетах, использован коэффициент 1,2.
| сеть | показат. | содерж. | разность | руда, тт | разность | Au, кг | разность |
| 15х30 | 2,196 | 0,011 | 888,9 | 32,6 | 1952,2 | 61,5 | |
| 2,175 | 0,01 | 954,2 | 32,7 | 2075,1 | 61,4 | ||
| среднее | 0,0105 | 32,65 | 61,45 | ||||
| отн. сред | 0,0048 | 0,035431 | 0,030516 | ||||
| стандарт | 0,00577 | 0,042518 | 0,036619 | ||||
| 30х30 | 2,132 | 0,053 | 1058 | 136,5 | 2255,6 | 241,9 | |
| 2,228 | 0,043 | 850,3 | 71,2 | 1894,7 | 119 | ||
| 2,165 | 0,02 | 899,8 | 21,7 | 1994,7 | 19 | ||
| 2,228 | 0,043 | 878 | 43,5 | 1955,9 | 57,8 | ||
| среднее | 0,03975 | 68,225 | 109,425 | ||||
| отн. сред | 0,018192 | 0,074037 | 0,05434 | ||||
| стандарт | 0,021831 | 0,088844 | 0,065208 | ||||
| 30х60 | 2,069 | 0,116 | 983,9 | 62,4 | 2035,7 | 22 | |
| 2,242 | 0,057 | 912,1 | 9,4 | 2044,6 | 30,9 | ||
| 2,116 | 0,069 | 909,1 | 12,4 | 1924,1 | 89,6 | ||
| 2,092 | 0,093 | 735,6 | 185,9 | 1634 | 379,7 | ||
| 2,282 | 0,097 | 815,6 | 105,9 | 1861,4 | 152,3 | ||
| 2,213 | 0,028 | 843,9 | 77,6 | 1867,3 | 146,4 | ||
| 2,143 | 0,042 | 1206,9 | 285,4 | 2587 | 573,3 | ||
| 2,332 | 0,147 | 965,1 | 43,6 | 2251 | 237,3 | ||
| среднее | 0,081125 | 97,825 | 203,9375 | ||||
| отн. сред | 0,037128 | 0,106158 | 0,101275 | ||||
| стандарт | 0,044554 | 0,12739 | 0,12153 |
Таблица 3. Расчет погрешностей по результатам разрежения сети
Полученные на основе эксперимента результаты разрежения требуют введения поправок за собственные ошибки модели. Последние в данном случае принимаются максимальными, то есть не учитывают возможное влияние закономерного изменения геологоразведочных параметров в пространстве. Поправки вводятся за счет суммирования относительных дисперсий, полученных по эксперименту и по исходной сети. Результаты расчетов приведены в таблице 4.
| сеть | статистич. параметры | содержание | запас руды | запас золота | |||
| исходная | отн. погрешность | 0,04 | 0,0483 | 0,0549 | |||
| отн. дисперсия | 0,0016 | 0,00233 | 0,003 | ||||
| 15х30 | эксп.отн. погрешность | 0,00577 | 0,0425 | 0,0366 | |||
| эксп. отн. дисперсия | 0,00003 | 0,00181 | 0,00134 | ||||
| расч. отн.погрешность | 0,04 | 0,064 | 0,066 | ||||
| расч. отн. дисперсия | 0,00163 | 0,00414 | 0,00434 | ||||
| 30х30 | эксп. отн. погрешность | 0,0218 | 0,0888 | 0,0652 | |||
| эксп. отн. дисперсия | 0,000618 | 0,00789 | 0,00425 | ||||
| расч. отн.погрешность | 0,0471 | 0,1011 | 0,0851 | ||||
| расч. отн. дисперсия | 0,00222 | 0,01022 | 0,00725 | ||||
| 30х60 | эксп. отн. погрешность | 0,0446 | 0,1274 | 0,1215 | |||
| эксп. отн. дисперсия | 0,00217 | 0,01623 | 0,01476 | ||||
| расч. отн.погрешность | 0,0614 | 0,1362 | 0,1333 | ||||
| расч. отн. дисперсия | 0,00377 | 0,01856 | 0,01776 |
Таблица 4. Расчет относительных погрешностей оценки подсчетных параметров с учетом собственных ошибок модели
В реальных ситуациях исследования по разрежению сети могут быть проведены на участках различных размеров; результаты будут зависеть от количества (запасов) руды в их пределах. Возможность сопоставления разнородных данных обеспечивается приведением рассчитанных погрешностей к нормативному объему недр. Современные подходы к оценке разведанности месторождений предлагают принимать в качестве нормативного объекта блоки, сопоставимые по запасам руды годовой (или квартальной) производительности предприятия. В данном случае годовая производительность рудника для месторождения принимается равной 1000 тыс.т. Таким образом, соотношение запасов руды на участке детализации и в блоке годовой производительности составит 921,5/1000 = 0,92. Величина поправочного коэффициента К, учитывающего влияние этого фактора, в соответствии с правилами математической статистики определяется как корень квадратный из величины рассчитанного соотношения запасов: К=√0,92 = 0,96. Результаты пересчета величины погрешностей в оценке параметров при сети различной плотности приведены в таблице 5.
| сеть | погрешность | содержание | запас руды | запас золота | |||
| исходная | 0,04 | 0,0483 | 0,0549 | ||||
| с поправкой К=0,96 | 0,038 | 0,0466 | 0,0527 | ||||
| 15х30 | расчетная по эксперим. | 0,04 | 0,064 | 0,066 | |||
| с поправкой К=0.96 | 0,038 | 0,0614 | 0,0634 | ||||
| 30х30 | расчетная по эксперим. | 0,0471 | 0,1011 | 0,0851 | |||
| с поправкой К=0.96 | 0,0452 | 0,0971 | 0,0817 | ||||
| 30х60 | расчетная по эксперим. | 0,0614 | 0,1362 | 0,1333 | |||
| с поправкой К=0.96 | 0,0589 | 0,1308 | 0,128 |
Таблица 5. Пересчет величины погрешности на блок годовой производительности
Данные таблицы показывают, что величина ошибки в оценке среднего содержания в принятом диапазоне плотности сети изменяется от 3.8 до 5.6%. Запасы руды в этих же условиях оцениваются с ошибками от 4.7 до 13.1%; запасы металла – с погрешностями 5.3 – 12.8%.
Предложения отечественных авторов (4) говорят о том, что при погрешностях оценки параметров менее 10 % запасы можно квалифицировать по категории А и при погрешностях 10-20% по категории В. Этим требованиям отвечают, соответственно сеть 30х30м и 30х60м. Зарубежные исследователи (Г.Паркер, устное сообщение) считают, что запасам категории measured соответствует ошибка в оценке содержаний 5%, а запасам категории indicated – до 10%. Видно, что обсуждаемые параметры разведочных сетей удовлетворяют и этим требованиям.
Ошибки геометризации оценивались в разрезах по вариантам разрежения (рис. 2) через соотношение суммарной площади искажающих площадок (безрудные участки в разведочном контуре и рудные участки за его пределами) к удвоенной истинной площади рудного тела. Средние значения этого показателя, вычисленные с учетом всех вариантов наложения, составили для сети 30х60м – 31%, а для сети 30 х 30м – 16%. Собственная погрешность модели, по экспертной оценке, может составлять 5-6%. Таким образом, сеть 30х60м с позиций ошибок геометризации вполне удовлетворяет требования к категории С1, а сеть 30х30м – требованиям к категории В.

Рис. 2. Определение ошибок геометризации на разрезе по вариантам резрежения сети до 30 м.
Следует отметить, что разведка запасов категории С1 на данном месторождении проводилась по сети 20-30х50-60м. Проведенные по данной методике исследования показывают, что полученные выводы не противоречат практике ведения геологоразведочных работ. Подобные исследования позволяют корректировать параметры разведочной сети на отдельных участках в соответствии с целевым назначением подсчета и категоризации запасов.
Литература
- Требования к составу и правилам оформления представляемых на государственную экспертизу материалов по подсчету запасов месторождений твердых полезных ископаемых М, МПР, 2011г.
- Рациональная сеть предварительной разведки. М., Недра, 1978г.
- В.А.Викентьев, И.А.Карпенко, М.В.Шумилин. Экспертиза подсчетов запасов рудных месторождений. М., Недра, 1988г.
- Методические рекомендации по использованию количественных и вероятностных оценок точности и достоверности определения основных подсчетных параметров запасов месторождений твердых полезных ископаемых. М., ГКЗ, 2008 г.
П.И. Кушнарев — заместитель начальника отдела подсчета запасов ЗАО «Полюс»
Опубликовано в журнале “Золото и технологии” № 1(19)/март 2013 г.